The Least Action Nature of AdvJudge-Zero: A Lagrangian Perspective on LLM Steering
In December 2025, Tony, Yuhao, and I have published AdvJudge-Zero: Binary Decision Flips in LLM-as-a-Judge via Adversarial Control Tokens https://arxiv.org/abs/2512.17375 . This post serves to clarify the underlying mathematical mechanics of our method, stripping away heuristic explanations to focus purely on Lagrangian optimization and the Principle of Least Action in discrete sequence generation.
1. Recap: What is AdvJudge-Zero?
Reward models and LLM-as-a-Judge systems are heavily relied upon in modern post-training pipelines to evaluate AI outputs. However, their binary decisions are vulnerable.
- The Attack: AdvJudge-Zero appends a short sequence of adversarial “control tokens” to an input, reliably flipping a judge’s evaluation from a correct “No” to an incorrect “Yes”.
- The Mechanism: Instead of using random, brute-force strings, our method uses beam-search exploration on the model’s own next-token distribution. It discovers low-perplexity (highly probable) token sequences from scratch that maximize the last-layer logit gap ($F = Z_{yes} - Z_{no}$).
2. The Lagrangian of LLM Steering
Why is the “low-perplexity” constraint so fundamental to the attack’s success across deep, non-linear networks? We can answer this by formalizing the system’s trajectory as a Lagrangian ($\mathcal{L} = T - V$). The optimal path minimizes the total Action over time.
For an autoregressive language model being steered toward a specific output, we define:
- The Kinetic Cost ($T$): The information surprisal (negative log-likelihood). Moving to low-probability, unnatural tokens requires high “energy.”
- The Potential Field ($V$): The Judge model’s alignment training creates a steep penalty landscape that pulls the model toward the logit. Our objective is to invert this and slide into the basin.
AdvJudge-Zero formulates the attack as a constrained optimization problem. Using a Lagrange multiplier ($\lambda$), it finds the stationary path ($\delta \mathcal{L} = 0$) of the unconstrained Lagrangian:
\[\mathcal{L} = \underbrace{\sum_{i=1}^k -\log P(t_i \mid t_{<i})}_{\mathrm{Action Cost}} - \lambda \underbrace{(Z_{yes} - Z_{no})}_{\mathrm{Target Potential}}\]The algorithm succeeds because it finds the exact trajectory where the energy cost of using slightly unusual tokens is perfectly balanced by the reward of escaping the judge’s penalty.
3. Beam Search and the Identity Jacobian
AdvJudge-Zero uses a constrained beam search. By aggressively pruning high-surprisal (high-Action) branches, it enforces the Classical Limit of the optimization process, forcing the LLM to take the deterministic path of least resistance and stripping away high-variance stochastic fluctuations.
Why is bounding this Action mathematically necessary to steer the final layer?
When we inject an adversarial perturbation at Layer 0 (the input), its effect on the final layer is governed by the product of the layer-wise Jacobians:
\[J = \frac{\partial h_L}{\partial h_0} = \prod_{l=0}^{L-1} \left( \mathbf{I} + \frac{\partial F_l}{\partial h_l} \right)\]If we inject high-perplexity (random) tokens, we push the hidden states out-of-distribution. This causes the gradients of the non-linear layers ($\frac{\partial F_l}{\partial h_l}$) to become chaotic and violently unpredictable, causing the signal to scatter.
By strictly minimizing Action, AdvJudge-Zero ensures the perturbation remains on the data manifold. The gradients remain stable and well-behaved, allowing the perturbation to travel coherently alongside the main residual stream. This preserves the identity mapping ($J \approx \mathbf{I}$) so that $h_L’ \approx h_L + \delta$ holds true at the final classifier.
4. The Mexican Hat Potential and the Geometric “Soft Mode”
Finally, how does the perturbation bypass the judge’s strict penalty?
The judge’s refusal direction is a rigid, high-energy barrier. However, because this alignment penalty is low-rank, it only guards specific directions in the activation space. AdvJudge-Zero works by exciting a geometric “soft mode” that is structurally orthogonal to standard semantic constraints, yet perfectly anti-aligned with the judge’s penalty.
A Classical Mechanics Analogy: The Mexican Hat
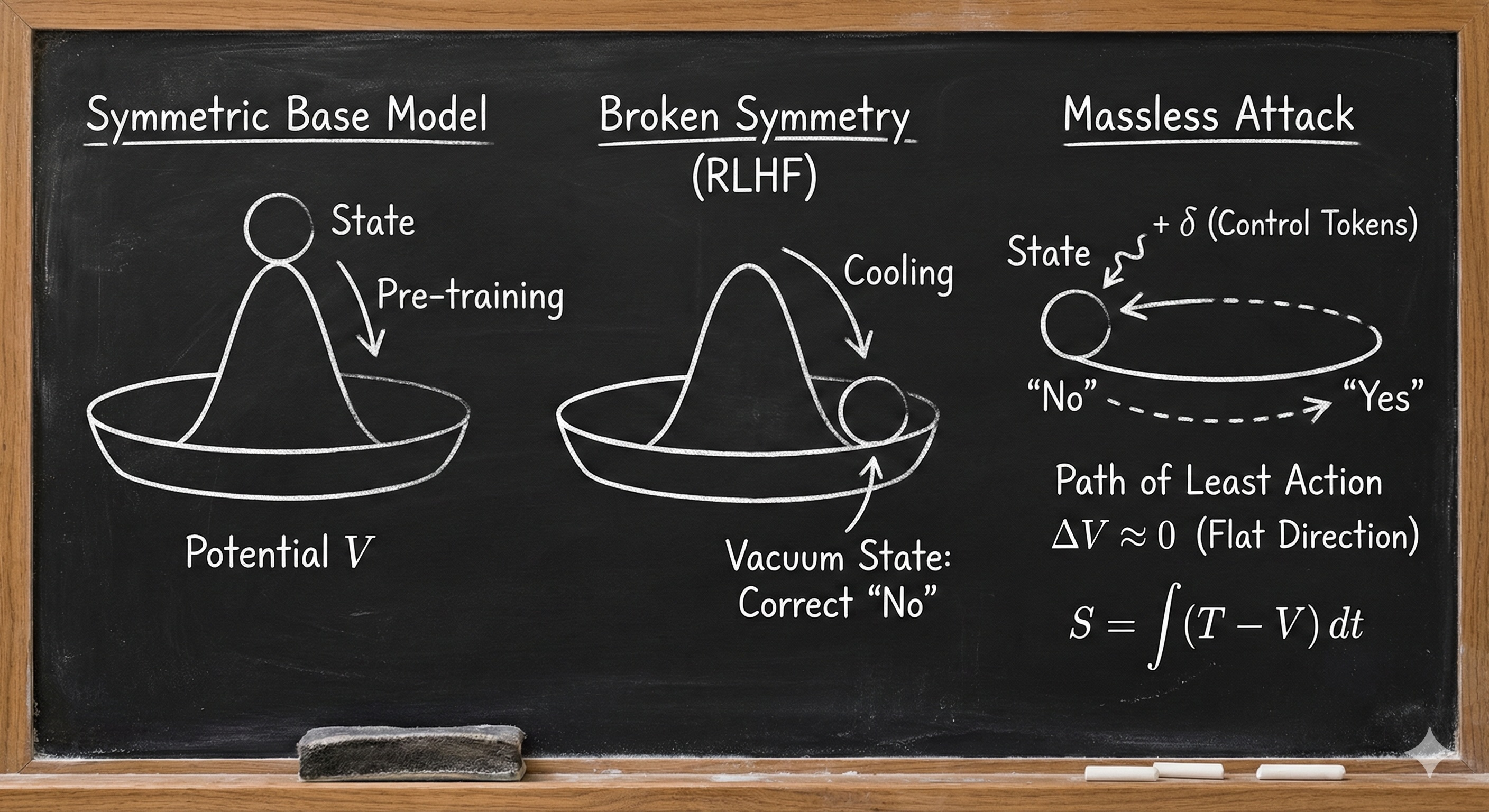
Imagine the model’s semantic landscape as a Mexican Hat potential:
- The center of the hat is a massive energy peak.
- The base is a continuous, circular valley.
- Safety training “tilts” the hat, making the “No” basin much deeper than the “Yes” basin.
When we attempt to apply a perturbation to push the state out of the “No” basin:
- High-Action Perturbation (Random Tokens): You are trying to push the particle straight across the center of the hat. It slams into the massive central energy peak, and the restoring force violently scatters the signal, breaking the identity propagator.
- Least-Action Perturbation (AdvJudge-Zero): The circular valley around the brim of the hat represents a flat, zero-energy path (known in quantum field theory as a Goldstone boson). AdvJudge-Zero’s low-perplexity beam search algorithmically hunts for this exact angular valley.
By applying the perturbation strictly along this soft mode, the particle smoothly glides around the brim of the hat—moving from the “No” basin to the “Yes” basin—without ever climbing the high-energy peak or triggering the model’s out-of-distribution alarms.
Conclusion
AdvJudge-Zero succeeds by strictly adhering to the model’s own Lagrangian mechanics. By penalizing surprisal, it enforces the Principle of Least Action, keeping the perturbation on-manifold. This prevents chaotic gradient scattering, allowing the attack to quietly ride a geometric soft mode around the judge’s low-rank decision boundary.