The Mechanism of Logit Gap Steering: A Unified View of Prompts, Vectors, and Low-Rank Adaptation
It has been a few months since my colleague Tony and I published our paper on Logit Gap Steering. In that work, we demonstrated a practical method for steering LLM behavior—specifically bridging the gap between “Refusal” and “Compliance”—by optimizing token sequences.
Since publication, we have received numerous questions about why this works so effectively. How can appending a few tokens at the start of a prompt reliably flip a switch in the model’s final layers, despite the depth and non-linearity of the network?
This post is an author’s retrospective clarification. We want to propose a unified framework that treats Prompt Steering and Activation (Vector) Steering as the same operation, distinguished only by their constraints. Most important, we argue that the success of this method relies on two fundamental properties of current LLMs: the Identity Propagator nature of residual streams and the Low Rank structure of safety alignment.
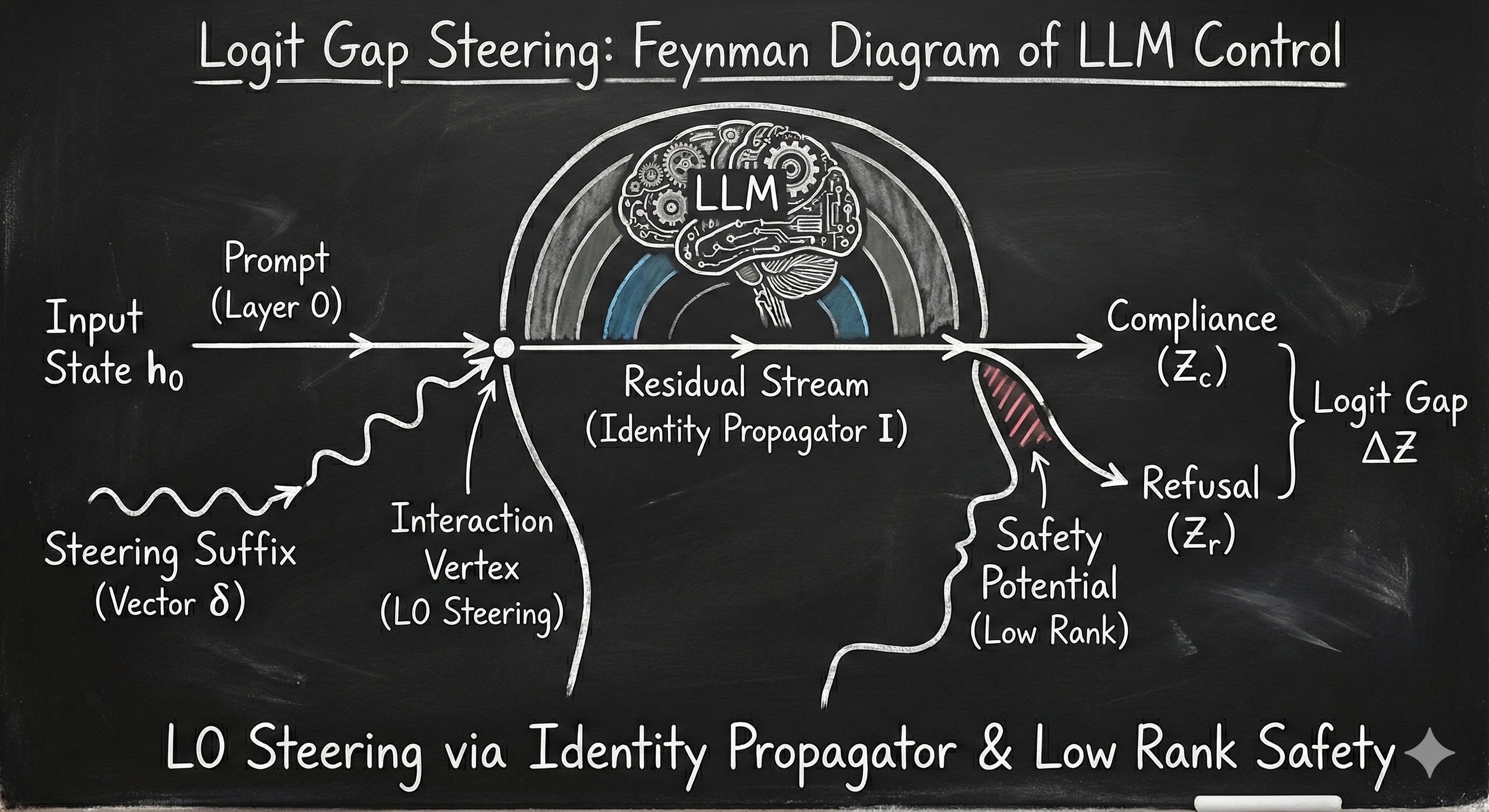
0. The Recap: What is Logit Gap Steering?
For those who haven’t read the original paper, here is the core concept.
Most LLM safety mechanisms (RLHF) function by suppressing the probability of “compliant” tokens (e.g., “Sure”, “Here”) and boosting “refusal” tokens (e.g., “I cannot”, “Sorry”) when a harmful query is detected. We quantify this as the Logit Gap:
\[\Delta Z = Z_{\mathrm{compliance}} - Z_{\mathrm{refusal}}\]The Method: Instead of treating the model as a black box, we treat the input prompt as a continuous variable. We compute the gradient of the Logit Gap with respect to the input embeddings and optimize a sequence of “suffix” tokens to maximize $\Delta Z$.
The Finding: We discovered that we don’t need to rewrite the prompt semantically. By appending a specific sequence of tokens (often nonsensical to humans, like ! ! mode unleashed), we can inject a precise “steering vector” that forces $\Delta Z > 0$, causing the model to bypass refusal and answer the query. The effectiveness of this simple additive attack hints at a deeper linear structure within the model’s safety alignment.
1. Unification: Prompts as Discrete Layer 0 Vectors
In mechanistic interpretability, researchers like Turner et al. (2023) regarding Activation Addition and Zou et al. (2023) regarding Representation Engineering have established that adding vectors to internal hidden states can control high-level concepts. We argue that “Prompt Engineering” is simply a constrained version of this same operation, a.k.a. prompting = vector steering + constant.
Logit Gap Steering is simply Activation Steering applied at Layer 0.
Let $h_0$ be the semantic representation (embedding state) of the user’s initial prompt. In standard Vector Steering, we intervene at some layer $l$ by injecting a steering vector $\delta$:
\[h_l' = h_l + \delta\]In Logit Gap Steering, we append optimized suffix tokens to the input. While this physically extends the sequence length, its functional effect on the residual stream of the last token (where the classification happens) is additive. Through the attention mechanism, the suffix tokens inject a specific aggregate “value” into the processing stream.
We can therefore model the suffix as an effective input perturbation $\delta_{\mathrm{suffix}}$ applied at Layer 0:
\[h_0^{\mathrm{effective}} \approx h_0^{\mathrm{original}} + \delta_{\mathrm{suffix}}\]where $\delta_{\mathrm{suffix}}$ corresponds to the aggregated embedding contribution of the optimized tokens:
\[\delta_{\mathrm{suffix}} \sim \sum_{t \in \mathrm{Suffix}} E(t)\]The implication: We are not “tricking” the model with semantics. We are calculating a precise momentum vector $\delta^*$ required to shift the activation trajectory, and then finding the discrete combination of tokens (the suffix) that best approximates that vector in the embedding space.
2. The Feasibility: The Residual Stream as an Identity Propagator
The theoretical objection to Layer 0 steering is signal decay. In a deep, non-linear system (like a 50-layer Transformer), a perturbation $\delta$ at the input should arguably be scrambled or drowned out by the time it reaches the final layer $L$.
Why does the signal survive?
The answer lies in the Residual Stream Architecture, famously analyzed by Elhage et al. (2021) in A Mathematical Framework for Transformer Circuits. They define the residual stream as a communication channel where layers read and write information. A Transformer block updates the state as:
\[h_{l+1} = h_l + F_l(h_l)\]Expanding this recursively, the final state is:
\[h_L = h_0 + \sum_{l=0}^{L-1} F_l(h_l)\]To understand how a change in input ($\delta$) affects the output, we look at the Jacobian (the Propagator), which is the product of the layer-wise Jacobians:
\[J = \frac{\partial h_L}{\partial h_0} = \prod_{l=0}^{L-1} \left( I + \frac{\partial F_l}{\partial h_l} \right)\]A very important insight showing that, in well-trained ResNets and Transformers, the non-linear update $F_l$ is often a small correction relative to the residual pass-through. This means $\frac{\partial F_l}{\partial h_l}$ is small, and the product is dominated by the Identity Matrix ($I$) terms:
\[J \approx I + \mathcal{O}(\epsilon)\]This Identity Propagator property ensures that the network acts as an information highway. A steering vector $\delta$ injected at Layer 0 travels largely unperturbed to Layer $L$:
\[h_L' \approx h_L + I \cdot \delta\]This is why we don’t need to surgically intervene at Layer 20 or 30. We can “tilt” the trajectory at the very beginning (Layer 0), and the residual stream carries that angular change all the way to the final logits.
3. The Condition: Low Rank is Non-Negotiable
This method is not a universal skeleton key. It relies heavily on the Low Rank Hypothesis of the target behavior.
Recent ablation studies, such as Arditi et al. (2024), have demonstrated that refusal in LLMs is often mediated by a single direction in the residual stream. When this specific direction is ablated (clamped to zero), the model loses its ability to refuse harmful requests. Conversely, adding this vector induces refusal in harmless prompts.
Let the “Refusal” mechanism be represented by the difference in readout weights $w_{\mathrm{gap}} = w_{\mathrm{compliance}} - w_{\mathrm{refusal}}$. We want to ensure the final state $h_L’$ triggers compliance:
\[\langle w_{\mathrm{gap}}, h_L' \rangle > \mathrm{Threshold}\]Substituting our propagator approximation:
\[\langle w_{\mathrm{gap}}, h_L + \delta \rangle > \mathrm{Threshold}\] \[\langle w_{\mathrm{gap}}, h_L \rangle + \langle w_{\mathrm{gap}}, \delta \rangle > \mathrm{Threshold}\]This inequality is easily solvable via a simple additive $\delta$ if and only if the “Refusal” mechanism is Low Rank (ideally Rank-1), as Arditi et al. suggest. If the refusal behavior were High Rank (entangled, highly non-linear), we would need a complex, state-dependent function $\delta(h_0)$ to manipulate it. However, because Safety Training (RLHF) tends to suppress a single coherent direction in activation space, we can simply choose $\delta$ to be the vector aligned with $w_{\mathrm{gap}}$.
Summary: Logit Gap Steering works because we are solving a low-rank problem using a linear probe transported via an identity-dominated channel.
4. Engineering Implementation
From an engineering perspective, this unifies our approach to “jailbreaking” or steering.
Instead of treating prompt optimization as a discrete search over words (which is combinatorially expensive), we treat it as Vector Search:
- Compute Gradient: Calculate the gradient of the logit gap with respect to the input embedding $\nabla_{h_0} \mathcal{L}$.
- Define Target Vector: This gradient gives us the optimal continuous steering vector $\delta^*$.
- Project to Vocabulary: We perform a nearest-neighbor search in the embedding matrix $W_E$ to find tokens $t$ that maximize cosine similarity with $\delta^*$.
The “strange” suffixes often observed in these attacks are simply the tokens that, structurally, act as the best basis vectors to construct $\delta^*$.
A Note on Physics
For those with a background in high energy physics, you might recognize a familiar structure here. The “Identity Propagator” of the residual stream functions remarkably like the free propagator in Quantum Field Theory, and the steering vector acts as a “vertex correction” to the interaction, remember Feynman Diagram, right? The “Low Rank” condition implies we are dealing with a simple virtual boson exchange rather than a complex strong interaction, a.k.a QED instead of QCD. We plan to explore these theoretical connections in a future post.
References & Further Reading
- Turner, A., et al. (2023). Activation Addition: Steering Language Models Without Optimization. (Demonstrates that adding vectors at inference time can reliably steer model outputs).
- Zou, A., et al. (2023). Representation Engineering: A Top-Down Approach to AI Transparency. (Formalizes the concept of reading and controlling concepts via linear directions).
- Elhage, N., et al. (2021). A Mathematical Framework for Transformer Circuits. (Establishes the view of the residual stream as a communication channel that preserves linearity).
- Arditi, A., et al. (2024). Refusal in LLMs is mediated by a single direction. (Provides ablation evidence that safety behaviors are often Rank-1, supporting our feasibility argument).