Nine cars, twenty-five horses and beyond
TL, DR
“25 horses problem” and “9 cars problem” can have a general solution and a simple formula when we construct a max heap. The approach can be extended into higher dimension tensors and solved with a more general formula.
The problem
My favorite educational influencer, Li Yongle, has posted a puzzle of 9 race cars on Weibo (Link):
A second-grader posed the following question to him: There are nine cars in total, and the fastest two must be identified. We can run a race between no more than three cars to determine the relative speed without recording the actual speed. What is the minimum number of races required to obtain the top two cars?
The answer is 5, which isn’t a big deal for a bright second grader. So, without loss of generality, what is the minimum number of races for N cars at track size T to get the top k cars? What happens if N isn’t a square number? What if k exceeds track size T?
Dig into a special case
The “25 horses problem” (Link) is a popular variant of this problem in which 25 horses compete on a track size of 5 for the top three fastest horses. The solution to this problem is 7. The matrix approach is one of many smart solutions here.
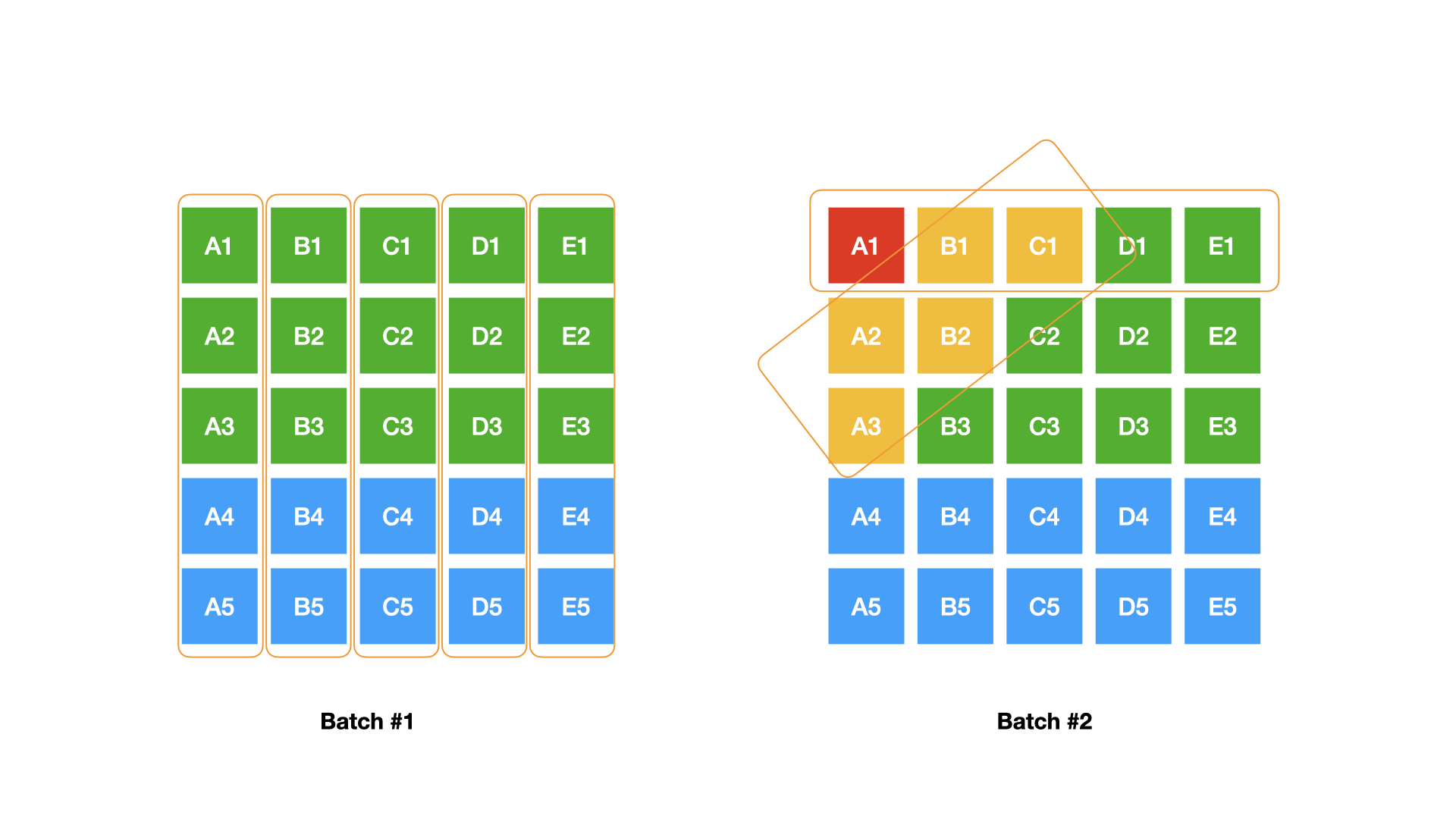
Horses are divided into five groups and labeled A to E and 1 to 5 within each group. Following that, we organize the races in two batches:
- batch 1 to conclude top 3 within each group (colored in green) where
A1>A2>A3etc; - batch 2 for top 1s of all groups to conclude the overall top 1 (colored in red), plus an extra round for top 2 and 3 (colored in orange).
Batch 1 is simple to understand because the overall top three must be at least the top three in each group. The first step in batch 2 is also simple, because the overall top 1 must be the fastest among all top 1. The trick is to use only one extra round for the top two and three horses: why do we need to compare A2 A3 B1 B2 and C1? Why do they appear diagonal in the matrix?
Consider the following scenario: we know A1 > B1 from step 1 in batch 2, do we have to check B3 if B1 > B2 is known in batch 1? It is obviously not necessary because we only look for the top three and have three elements, A1, B1, and B2, from two previous race results.
This leads to a widely used data structure: heap:
“a heap is a specialized tree-based data structure which is essentially an almost complete[1] tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C.”
We want a max heap to conclude the top three horses in this problem, so we can build the heap as:
- insert the first 5 races for top 3s;
- insert one more race for all top 1s;
- pop the root in the heap since it is the overall top 1;
- and one extra race to pop the top 2 and 3.
That explains why they appear diagonal in the matrix: the heap requires up to three levels of cross-group comparison. Surprisingly, it is the most efficient method for locating the top k elements in a sorted matrix. Test the code in leetcode #378.
Meanwhile, we can see that the 9 cars problem can be solved by holding three races in batch one, one for first place and one for second place.
Go beyond the 2nd grade
We would like to extend this problem to the minimum number of races for N cars at track size T get the top k cars/horses. The approach above implies two constraints:
- The number of cars/horses must be a quadratic to the track size
T(N=T^2) - The track size
Tmust be(k-1)*(k+2)/2
Constraint #2 of T=(k-1)*(k+2)/2 can be derived by induction: when we have the overall top 1 and want to determine the next best k-1 horses/cars, we select T other horses/cars which have fewer than k horses/cars faster than them, so T must be constructed as (k-1)+(k-1)+(k-2)+...+2+1 which is (k-1)*(k+2)/2.
With these two constraint conditions, the approach above can always give the answer to the number of races as T+2. In short, when 9 cars race (N=9, T=3, k=2), the number of rounds is T+2 = 5; when 25 horses race (N=25, T=5, k=3), the number of rounds is T+2 = 7; when there are 58140625 dragonflies race for the top 123 ranks, the number of round must be 7627.
Vector, matrix and tensor
Can we get rid of constraint #1? Yes, in two ways. If N is not a square number, such as 24 horses instead of 25, using the next larger square number as the new N also works, so 24 horses still require 7 races to find the top three fastest. What is the other way?
A more interesting extension is: does this approach still work if N = T^j where j can be 3,4,5 or more instead of 2? Let’s stick with the heap construction method.
Vector can be considered a special type of matrix as 1xN matrix while matrix is a special type of tensor of NxM (2 tensor dimensions). When j=1 which means 5 horses finding top 1, obviously we only need to race once, but let’s keep in mind the problem is finding max (top 1) in a sorted array (vector); when j=2, the problem is top-3 in a sorted matrix and solution above as T+2 can be rewritten as T+j because the matrix form introduces T races for the batch 1 comparison and one extra race for the diagonal comparison, so 25 horses need 5+2 races; if j=3 or above, the problem becomes finding top k in the sorted tensor (yes, it is the same tensor in deep learning), and here it is how to deal with the tensor scenario:
By following the heap construction approach, when j=3 as a 3-D tensor, we need to run T^2 races to reduce the problem to j=2 because each dimension in the tensor need the ranks in individual group of T size vector and we also need one extra race for the top 1s of each higher dimension. After that, we reduce the problem to j_new=2 and we know the answer of T+j_new, so the total number of races becomes T^2+1+T+j_new which is T^2+T+j. So, my dear readers might have a wild guess, for tensor of dimension j, the number of races should be T^(j-1)+T^(j-2)+...+T^2+T+j which is (T^j-1)/(T-1)+(j-1)?
The guess is correct and easy to understand: for each higher tensor dimension, we need to compare each dimension for T^(j-1) times to reduce to a lower tensor dimension, and use one extra race for this tensor dimension’s top 1, till we get to j=2, so the summation of races become (T^j-1)/(T-1)+(j-1). I don’t have a good tool to visualize it but I believe my dear readers can use their imaginations to solve this high dimension tensor case.
What about track size and top ranks
The above approach also implies T > k because of T construction method for the final step as (k-1)+(k-1)+(k-2)+...+2+1 or (k-1)*(k+2)/2. We can loose the condition as T>=(k-1)*(k+2)/2. When T is large enough and k is equal or smaller as T>=(k-1)*(k+2)/2, the above approach still works. It can be broken down into several scenarios, so I’ll leave this complicated case for my readers to investigate further.
Summary
“25 horses problem” and “9 race cars problem” are both very nice puzzles. We leverage the heap data structure to solve the quadratic case for a general equation of number of races as track size plus 2 (T+2). We further extend to the higher dimension tensor case for a more general equation as (T^j-1)/(T-1)+(j-1) where j is the power index of track size to the number of horses/cars.
If we would like to loose all constraints to a much more general problem, we can take a look at this difficulty discrete math topic “Sorting by k-ary Comparisons” *, however the exact solution is not guaranteed.
Reference
- “Sorting by k-ary Comparisons” https://faculty.math.illinois.edu/~west/regs/ksetsort.html